New Structured Map of Mixing Geometries

To mix cream into coffee, you can take several different approaches, according to the principles of physics: let the cream diffuse throughout the coffee by itself, gently stir it, or put a lid on the cup and shake it up.

Engineers often think about mixing according to those three approaches (diffusion, chaotic advection, and turbulence). But another approach called cutting and shuffling — think of cutting a deck of cards and shuffling it — offers another way to think about mixing.

Northwestern Engineering researchers have studied the mathematics behind such mixing and have recently come up with a new conceptual map to show how this approach works in different dimensions. They also introduce the concept of time-continuous piecewise isometries, a mathematical concept describing the way that the cut pieces can be rearranged to reform the original domain.

Their results, published recently in the journal Physics Reports, connects together years of research by the team about this new paradigm for mixing.

“This is a new way of looking at these mixing materials that could open up research in the field,” said Julio M. Ottino, Walter P. Murphy Professor of Chemical and Biological Engineering, who co-authored the research. Other authors include Richard Lueptow, professor of mechanical engineering; Paul Umbanhowar, research professor of mechanical engineering; and Lachlan Smith, a post-doctoral researcher.

Understand the dynamics of cutting and shuffling

Cutting and shuffling has emerged as an alternative way to think mathematically about mixing and has implications in how granular mixtures are mixed in spherical tumblers, as well as many other situations.

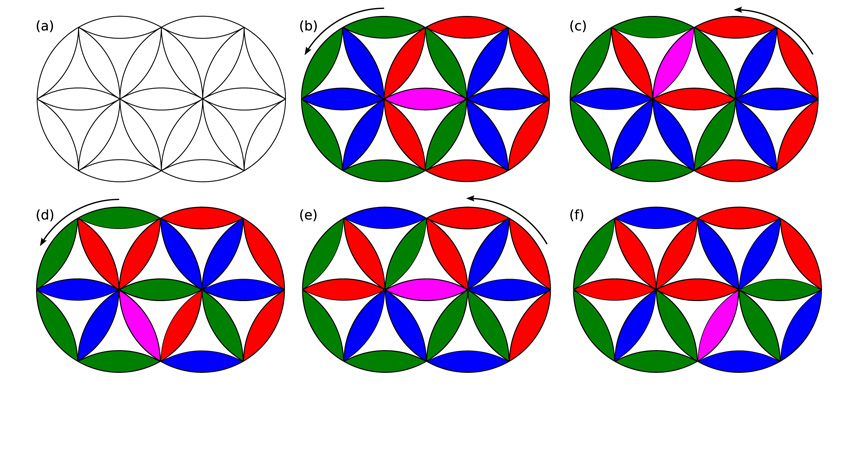
To think about mixing in this way, the researchers looked to the mathematics of piecewise isometries, a concept in which an object is cut into pieces and then the pieces are rearranged to re-form the original object. Examples include two-dimensional sliding circle puzzles, like the Cohan Circle, or three-dimensional “twisty puzzles,” like the Rubik’s cube.

“We know it’s very easy to mix the colors on a Rubik’s cube, and it’s much harder to put them back,” Lueptow said. “Most people think about the problem as putting the colors back, but we’re concerned with how they are mixed in the first place.”

Showing how geometries are related

The researchers have developed an approach that organizes how cutting and shuffling works in one, two, and three dimensions. They also describe how it works when the cutting and shuffling operation is time-continuous, meaning the object can be shuffled without losing its original shape, like a circular twisty puzzle, or non-time-continuous, like a Rubik’s cube. A Rubik’s cube is considered non-time-continuous because as you mix the colors, you need to rotate one of the sides outside of the original cube shape.

The result of the research is a mathematical organizational scheme that goes beyond toys to mixing solids and geophysics. By showing how these ideas fit together in a single structure, the investigators hope to open up the field to more research and to better understand how cutting and shuffling works when combined with other mixing techniques, like diffusion.

“Mixing in the context of piecewise isometries has not previously been studied in much detail,” Lueptow said. “We hope that showing how cutting and shuffling concepts are related to each other in different dimensions will be a springboard for further research.”