How Long Will it Take to Break Usain Bolt’s 100-meter Dash Record?

As Jamaican sprinter Usain Bolt takes his place on the starting block this weekend, his focus will likely be on performing his best – not on the statistical odds of breaking his own record.

But that’s exactly the sort of thing that Luís Amaral thinks about. Amaral, professor of chemical and biological engineering, was inspired by a recent article in 1843 magazine that claimed that Bolt’s 100-meter dash record was 20 years ahead of its time. The thinking of mathematician David Sumpter, the article’s author, is that between 1965 and 2005, the 100-meter dash world record improved from 10.06 seconds to 9.77 seconds, gaining an average of 0.007 seconds per year. Extrapolating the continuation of this improvement rate, would have predicted that the world record would break the 9.60 seconds mark around 2030.

Instead, four years later, Bolt established a new world record with a time of 9.58 seconds, a 0.19 second gain over the 2005 record. How was this possible? And when will the world record be beaten again?

According to Sumpter, it should take another 20 years. Amaral’s answer: it could take up to 230 years.

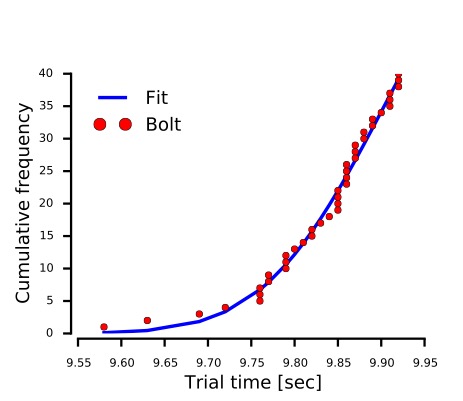In order to answer the first question, Amaral reviewed Bolt’s times for the 100-meter dash. The data looks surprising like a truncated Bell curve, with an estimated average trial time of 9.90 seconds and a spread of 0.155 seconds (see Figure A).

This meant Amaral could estimate the probability that Bolt would run the 100-meter dash for any desired time. For example, Amaral estimated that there is a 0.1 percent chance that Bolt will run the 100-meter in 9.57 seconds at the Rio Olympics.

Amaral further estimated that if Bolt runs 100 officially timed competitive 100-meter dashes, he has a 12 percent chance of beating his own record again. But Bolt will eventually lose the physical ability to perform at this level, and 100 races are a lot of races. (The typical sprinter runs perhaps 10 significant officially timed competitive races per year.)

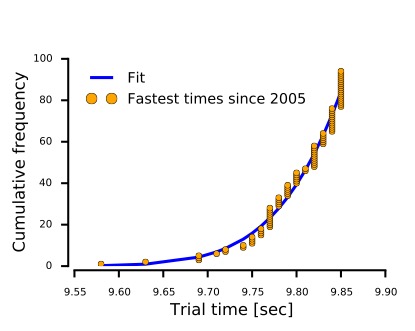
To estimate when the world record would be broken, Amaral did not consider a single sprinter, but the pool of current and future sprinters who on any given year have a chance of beating the current world record. The data for the fastest races run since 2005 is also well described by a truncated Bell curve, but with an average time of 9.98 seconds and a spread of 0.168 second. This distribution describes slower sprinters than Bolt, but it also attempts to capture the chance of someone as gifted as Bolt to appear in the future (see Figure B).

In order to estimate when the world record will likely be broken, Amaral needed to know how many capable sprinters there will be at any time and how many relevant races they will run per year. He assumed that, at any time in present and in the future, there would be a cohort of about 10 sprinters who can regularly run the 100-meter dash in less than 10 seconds. (The trial times obtained by participants in the 2012 Olympics show nine sprinters able to consistently complete the race under 10 seconds.) He also assumed that each of those sprinters runs the typical 10 officially timed, competitive races a year.

Thus, on average, there will be 100 races per year each with a probability of 0.00003 of achieving a trial time of, at most, 9.57 seconds.

Amaral then calculated how many races would have to occur in order for the probability that the record will be broken to become greater than the probability that it has not been broken. That occurs after about 23,000 races. Since he estimated that 100 relevant races will be run in a year, that means we may have to wait more than 230 years for the record to be broken.

But if Amaral assumes that the number of sprinters who can regularly run the 100-meter dash in less than 10 seconds will increase over time, than the estimated waiting time will decrease. If in the future there will be an average of 100 runners who on any given year are capable of breaking the current world record and that they each run 10 official meets per year, then the wait would be only 23 years.

“My expectation is that the waiting time will be closer to 230 years than 23 years,” he said.

Checking our estimation method: How frequent should trial times of 9.70 seconds or lower be?

The probability of a sprinter achieving a trial time of at most 9.70 seconds in a competitive race is approximately 0.0008. What is the number n of races after which it is likely that a time of 9.70 or lower is reached?

0.50 ~ 0.9992^n     =>     n ~ log 0.50 / log 0.9992     =>     n ~ 870

Using his current number of races/year (100), Amaral found that such as result should be observed every nine years or so. Conversely, since 2005, he expects to have observed about 12/9 ~ 1.3 trial times of 9.70 seconds or less. We have observed five, but three of those are due to Bolt, an exceptional sprinter who may come along once in a generation.