Research / Research AreasDiffusive Processes
Anomalous Diffusion
Most diffusion processes have been studied under the condition that diffusion is normal - that is, at the molecular level it is the result of independent random jumps (e.g., nearest-neighbor jumps) at regularly spaced time increments. In fact, the molecules can wait between successive jumps and can also execute not just nearest-neighbor jumps, but rather long jumps.
Both the waiting time distribution and jump size distribution must have finite moments. In some cases, however, these conditions are not met. Unlike normal diffusion, which is characterized by linear dependence of the mean square displacement of a randomly walking particle on time, anomalous diffusion is characterized by power laws with exponents not equal to one. If the exponent is less than one (greater than one), the diffusion process is slower (faster) than normal diffusion and is called "subdiffusive" ("superdiffusive").
Both types of anomalous diffusion processes have been recognized to play important roles in various physical, chemical, biological, and geological processes. For example, subdiffusion, which corresponds to molecules waiting for long times before jumping (i.e., with a waiting time distribution having infinite moments) often occurs in gels and polymers, while superdiffusion occurs in systems where there are long jumps of particles (i.e., with a jump size distribution having infinite moments). It is typical of some processes in plasmas and turbulence, surface diffusion and others. Mathematical description of anomalous diffusion involves integro-differential equations rather than the traditional diffusion equation and is therefore quite complex.
Research Areas
- Anomalous diffusion-reaction systems
- Traveling waves and interfaces
- Applications to drug delivery problems
Faculty
Reaction-Diffusion Systems
Reaction-diffusion systems are ubiquitous in many branches of science and engineering and have been attracting the attention of scientists, engineers, and mathematicians for decades.
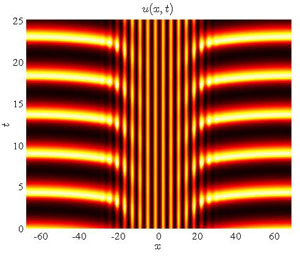Since the groundbreaking discoveries of Turing, who showed that diffusion in a mixture of chemically reacting species could cause instability of a spatially uniform state leading to the formation of spatio-temporal patterns, and Belousov and Zhabotinskii, who discovered oscillating chemical reactions, these systems have become one of the paradigms for the formation of spatio-temporal patterns in systems far from thermodynamic equilibrium. The formation of such fascinating structures as spiral waves, spatially-regular, stationary patterns with different symmetries (hexagonal, stripe, etc.), as well as chemical turbulence, have made reaction-diffusion systems the subject of numerous ongoing investigations.
Research Areas
- Reaction waves
- Pattern formation
- Propagation of interfaces
- Additional general mathematical models